Per visualizzare il workbook completo seguire il link: Cittadini Italiani Laureati emigrati Sankey | Tableau Public
L’obiettivo di questo post è riuscire a realizzare un grafico a dir poco particolare, non molto utilizzato sia per la mole di calcoli necessari per la costruzione che per la difficoltà di utilizzo all’interno di una dashboard. Il protagonista è il Sankey Chart, un tipo di grafico che permette di visualizzare flussi di dati tra più dimensioni.
Per la costruzione del grafico e la realizzazione di questo post è doveroso ringraziare la guida di Ian Baldwin presente sul blog di The Information Lab UK, visitabile con il seguente link: How to build a Sankey diagram in Tableau without any data prep beforehand – The Information Lab .
La caratteristica principale del Sankey Chart è la forma Sigmoide che assumono i flussi rappresentati, i quali hanno grandezza proporzionale alla quantità del flusso stesso.
Il primo passo verso la costruzione di questo grafico è la scelta di un dataset idoneo: si presta infatti molto bene alla visualizzazione di flussi di ogni tipo, come scambi di denaro, flussi migratori, in modo da dare risalto ai flussi con apporto dominante.
Ma cominciamo con la costruzione del grafico.
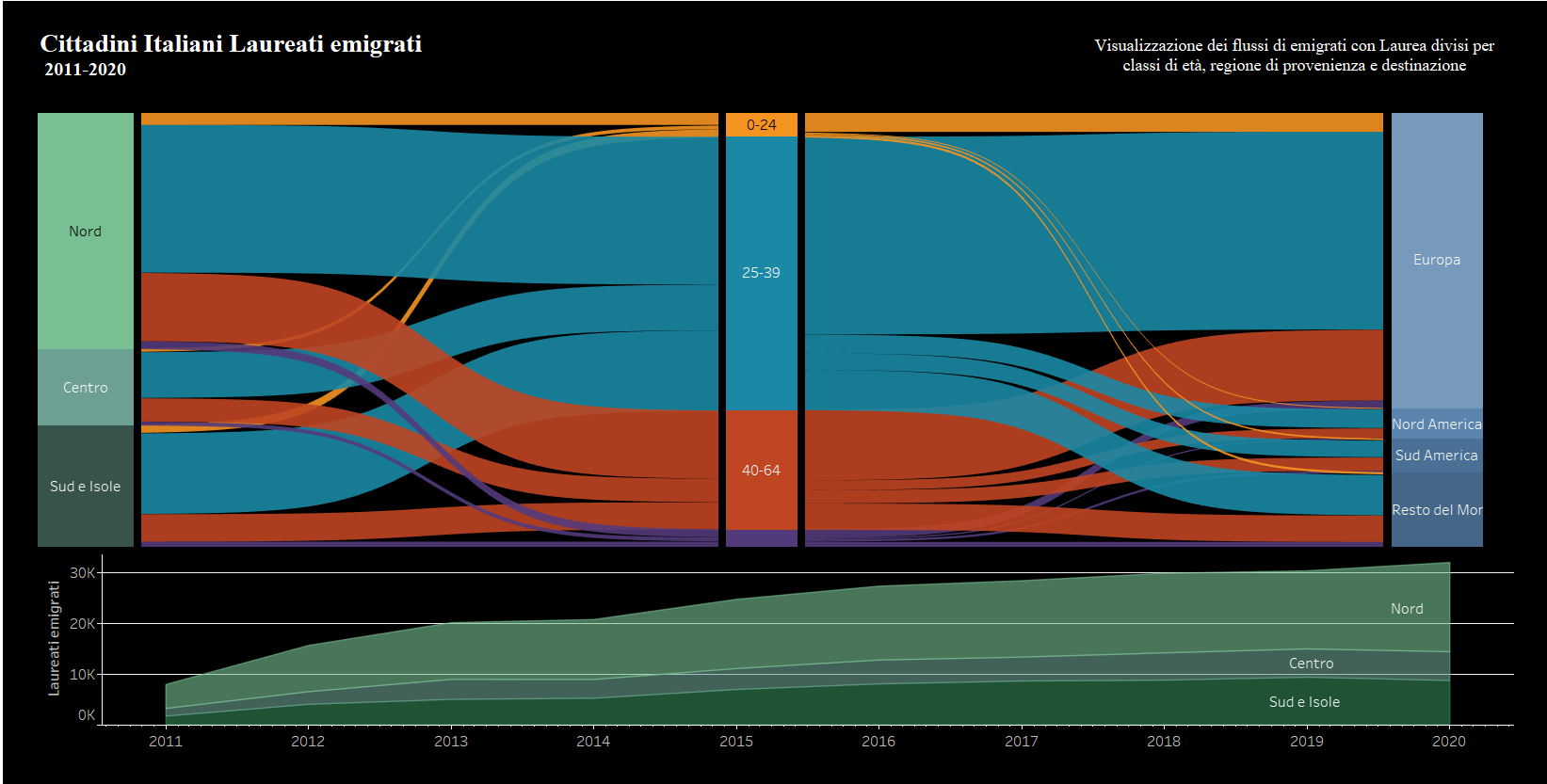
OBIETTIVO: Costruzione di un Sankey Chart per visualizzare il flusso migratorio degli Italiani laureati per fascia d’età e nazione di destinazione ( Trasferimenti di residenza (istat.it)).
PASSO 1: Parametrizzazione delle misure e delle dimensioni
Creare due parametri, chiamati [Select Dimension 1] e [Select Dimension 2], che costituiranno, nella visualizzazione, le colonne di partenza ed arrivo dei flussi. Si pongono in ogni parametro le stesse dimensioni, in modo da poter decidere successivamente cosa visualizzare sulla dashboard.
Si crea anche un campo calcolato con la misura scelta [Chosen Measure], nel caso specifico il numero dei cittadini emigrati.
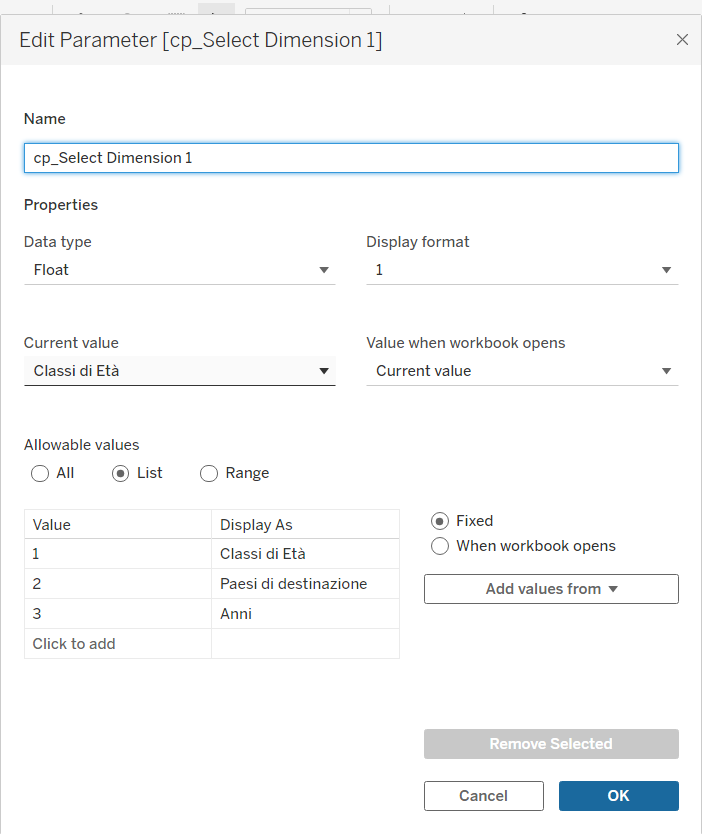
Per attivare i parametri creare due dimensioni, identiche nel contenuto tranne che per il parametro di riferimento.

PASSO 2: Densificazione dei dati
La densificazione è necessaria per popolare l’asse dove sarà plottata la dimensione. Per prima cosa creare la cornice del sentiero (Path Frame) che seguirà il flusso, e successivamente i contenitori (Bins) per inserire valori tra il punto minimo e massimo del flusso, in modo da unirli con il grafico. Nel caso specifico scelgo di creare 97 contenitori.
Path Frame
IF [Chosen Measure]={ FIXED :MIN([Chosen Measure])}
THEN 0
ELSE 97
END
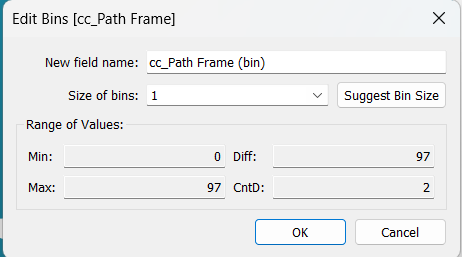
Contestualmente creare Path Index [Index() ] per fare calcoli sul sentiero del Sigmoide.
PASSO 3: Creazione della Sigmoide
Per questo passo è necessario costruire una variabile T che, a seconda del comportamento della misura scelta sul sentiero, si muove sull’asse orizzontale da un minimo di -6 ad un massimo di +6. Calcolare anche la funzione della Sigmoide in relazione a T.
T
IF [Path Index] < 50
THEN (([Path Index]-1)%49)/4-6
ELSE 12 - (([Path Index]-1)%49)/4-6
END
Sigmoid
1/(1+EXP(1)^-[T])
PASSO 4: Dimensione del Sigmoide
Come indicato nella prefazione, la caratteristica di questo tipo di grafico è la dimensione del flusso proporzionale alla dimensione del campione. Proprio per questo è necessario calcolare l’altezza del singolo sigmoide come il rapporto tra il valore e la somma di tutti i valori.
Sankey Arm Size
SUM([Chosen Measure])/TOTAL(SUM([Chosen Measure]))
PASSO 5: Calcolo delle linee del Sigmoide
Questo metodo prevede il calcolo delle linee superiori e delle linee inferiori di ogni singola curva. Nei calcoli Max è riferito alla curva superiore, Min alla curva inferiore, Position 1 alla Dimensione 1 e Position 2 alla Dimensione 2.
Max Position 1
RUNNING_SUM([Sankey Arm Size])
Max Position 1 Wrap
WINDOW_SUM([Max Position 1])
Max Position 2
RUNNING_SUM([Sankey Arm Size])
Max Position 2 Wrap
WINDOW_SUM([Max Position 2])
Max for Min Position 1
RUNNING_SUM([Sankey Arm Size])
Min Position 1
RUNNING_SUM([Max for Min Position 1])-[Sankey Arm Size]
Min Position 1 Wrap
WINDOW_SUM([Min Position 1])
Max for Min Position 2
RUNNING_SUM([Sankey Arm Size])
Min Position 2
RUNNING_SUM([Max for Min Position 2])-[Sankey Arm Size]
Min Position 2 Wrap
WINDOW_SUM([Min Position 2])
PASSO 6: Calcolo dei poligoni
Questo passo è necessario per la costruzione dei poligoni sulla base dei calcoli precedenti. Viene messa in relazione la funzione del sigmoide con il percorso compiuto dalla variabile.
Sankey Polygons
IF [Path Index] > 49
THEN [Max Position 1 Wrap]+([Max Position 2 Wrap]-[Max Position 1 Wrap])*[Sigmoid]
ELSE [Min Position 1 Wrap]+([Min Position 2 Wrap]-[Min Position 1 Wrap])*[Sigmoid]
END
PASSO 7: Preparazione del foglio di lavoro
Inserire Path Frame (bin) nelle righe, e selezionare dal menù “show missing value”, in modo da plottare a video la densificazione dei dati necessaria per la costruzione del grafico. È possibile vedere infatti tutti i contenitori numerati da 0 a 97, proprio come indicato nel Path Frame. Lo 0 corrisponde al Min Level of Detail della misura scelta, ed il 97 al valore diametralmente opposto.
Successivamente spostare in Detail nel Marks Panel la pills Path Frame (bin), già presente nelle righe. Inserire in Detail anche Dimension 1 e Dimension 2.
Inserire la variabile T nelle colonne (calcolare attraverso Path Frame (bin)).
Cambiare il Mark Type con Poligon ed trascinare Path Index in Path, sempre nel Mark Panel (calcolare anch’esso attraverso Path Frame (bin)).
PASSO 8: Sankey Poligon
Ora il passo a cui prestare più attenzione. Una volta inserito Sankey Poligons nelle righe è necessario settare le 12 Nested Calculation rispettando l’ordine mostrato nelle immagini successive.
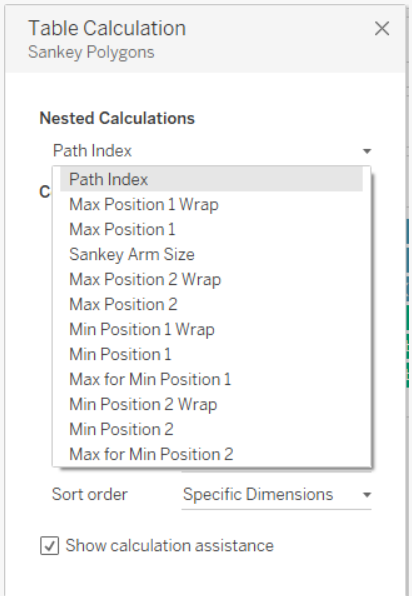
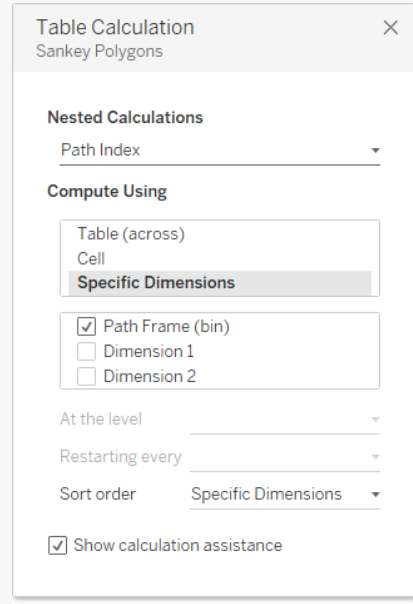
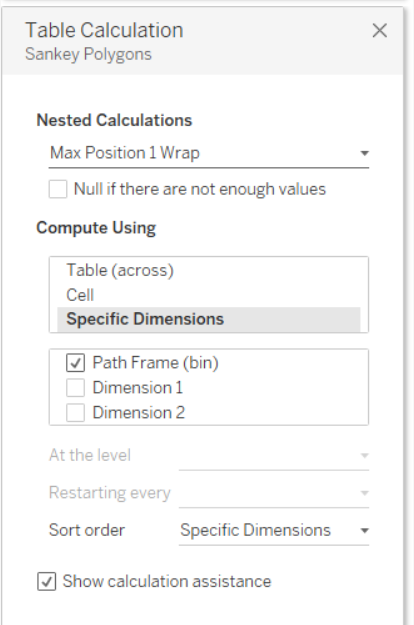
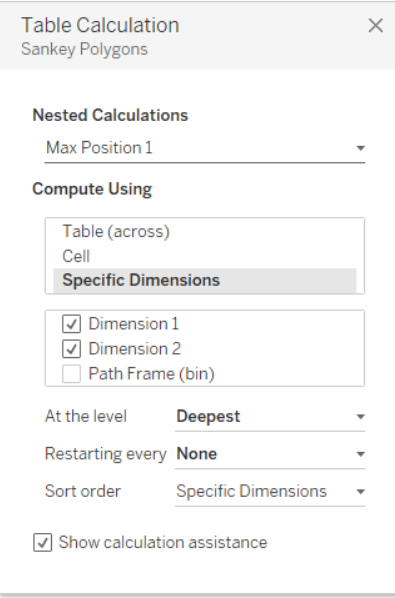
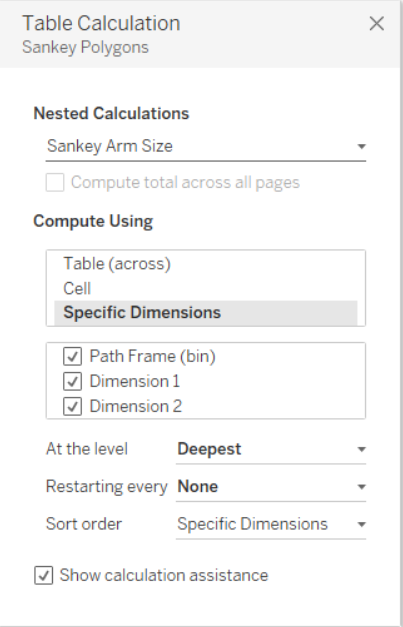
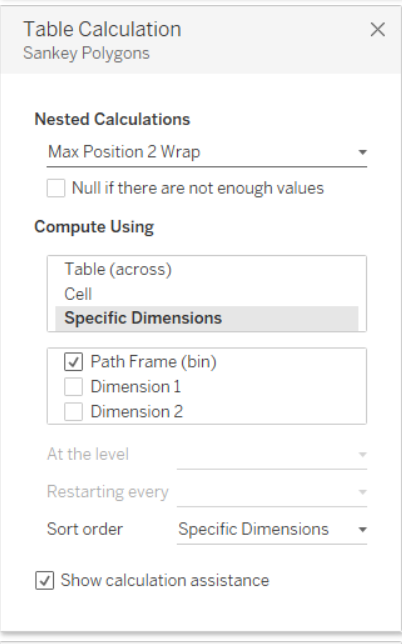
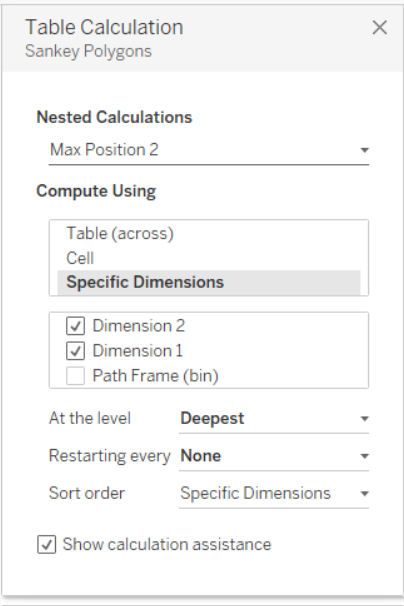
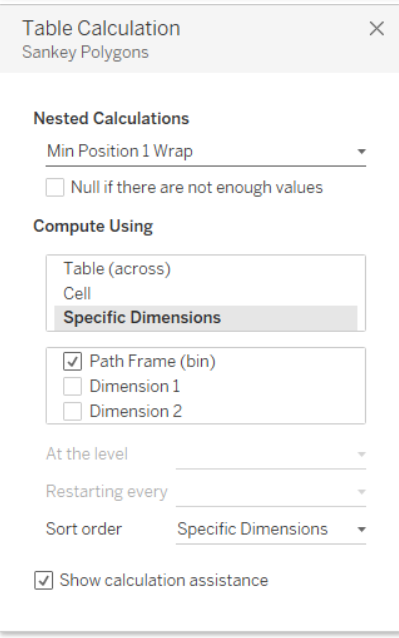
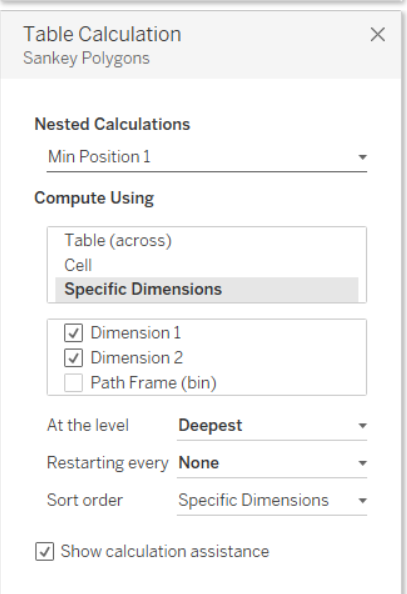
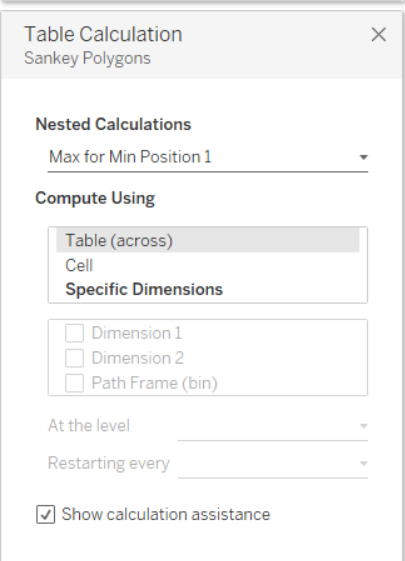
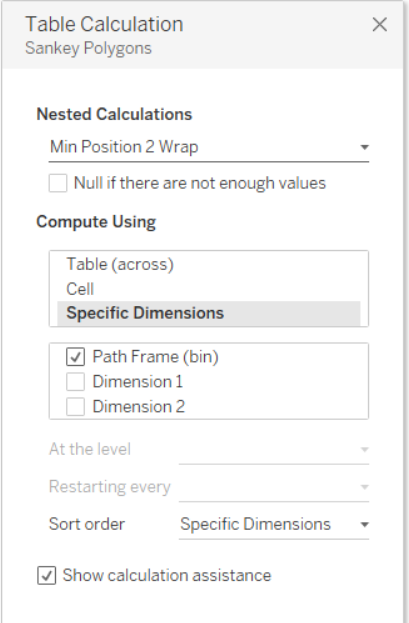
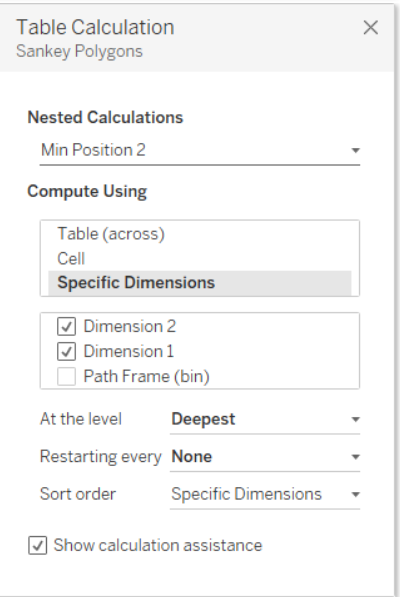
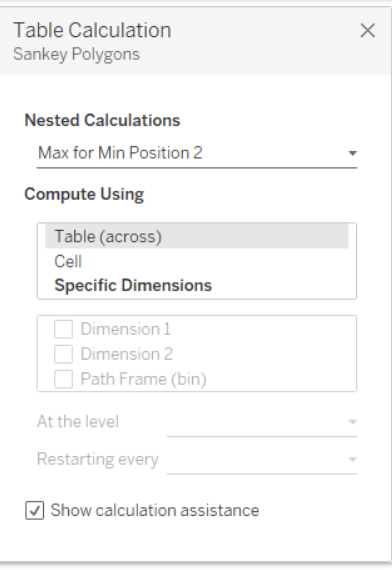
Una volta settate tutte le nested calculation, trascinare Dimension 1 su Color nel Mark Panel e il nostro Sankey Chart sarà pronto. Se il risultato finale non è simile a quanto mostrato, ripetere i passaggi precedenti, facendo attenzione non solo alla selezione dei valori giusti, ma anche all’ordine dei valori selezionati nel pannello del Tabel Calculation per tutte le nested calculation relative a Sankey Poligons.
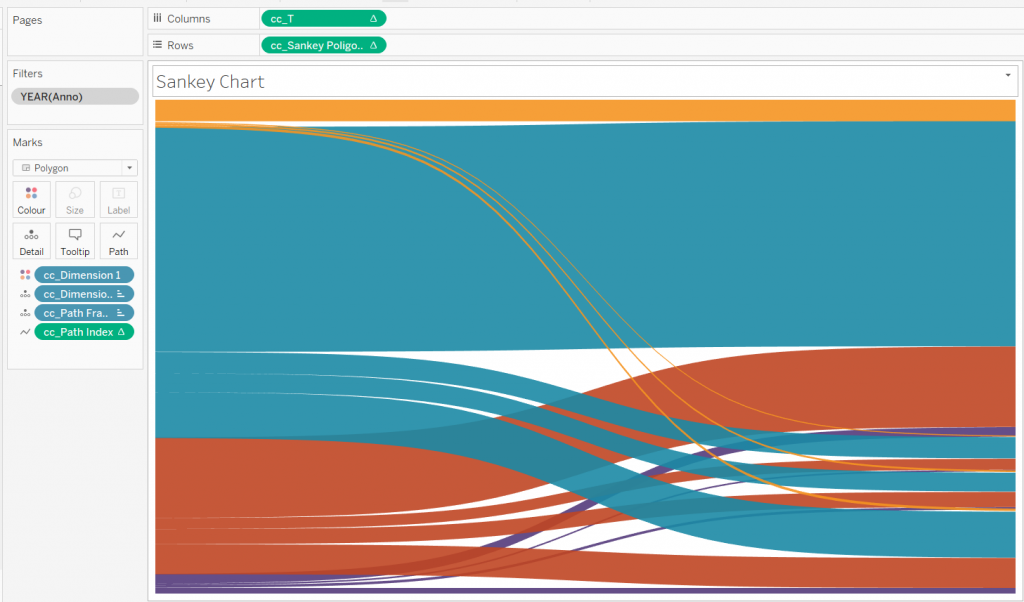
PASSO 9: Preparare la dashboard
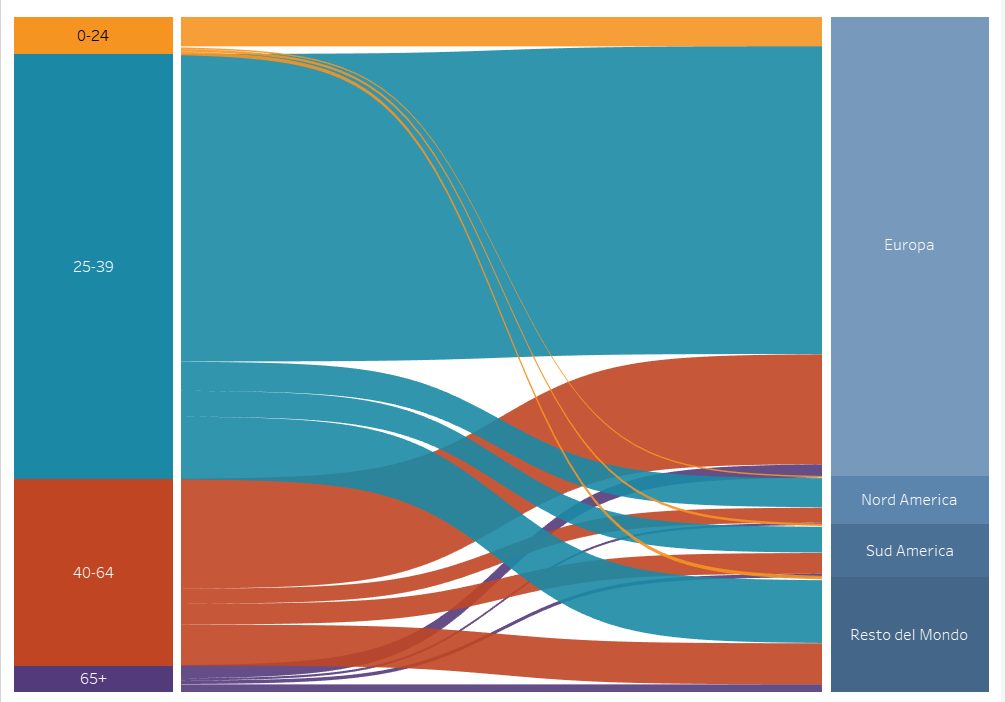
Per visualizzare nel migliore dei modi il Sankey Chart nella dashboard è buona prassi affiancarlo a due colonne, create con due stackbar con le Dimension 1 e 2, in modo da visualizzare il percorso della dimensione tra la due colonne.
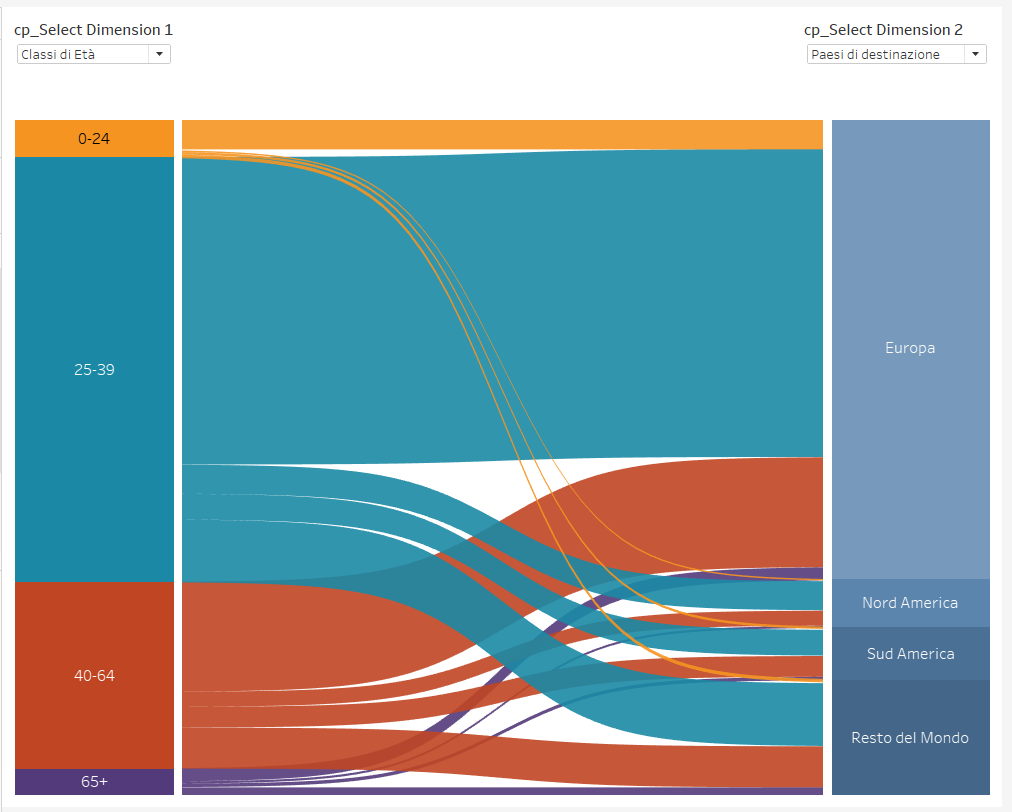
Nel caso in questione ho provveduto a creare un’ulteriore Sankey Chart specchiato al primo, in modo da avere il collegamento con una dimensione presente in un altro dataset (regione di partenza degli emigranti). Per creare il secondo Sankey Chart ho doppiato tutti i calcoli precedenti ad eccezione di Path Index, T e Sigmoid, che è possibile riutilizzare in quanto non dipendenti dalle Dimension scelte all’inizio del tutorial.
Il contenuto del grafico è filtrabile, fare attenzione però ad aggiungere i filtri al contesto, per renderli compatibili con il livello di dettaglio settato.